Advanced topics

Multiword and empty nodes

Multiword tokens are supported and can be accessed by calling n.multi_word. If n belongs to any multiword token, an instance of udon2.MultiWordNode will be returned, otherwise the accessor will return None. Mutators for multi-word nodes are currently not available. Getting a textual representation of a subtree (by calling n.get_subtree_text()) accounts for the multiword nodes. Each multiword node has three accessors: mw.min_id (the first ID of a multi-word expression), mw.max_id (the last ID of a multiword expression) and mw.token (the multiword token itself).

Empty nodes are currently ignored while reading CoNLL-U files.

Pruning vs ignoring

Suppose we want, as a step in text simplification, to split all coordinate clauses in a sentence into separate sentences. This requires identifying the nodes corresponding to the roots of coordinate clauses, by using the querying functionality from the previous section. Each clause should then be converted to a separate dependency tree, and all coordinate conjunctions should be removed. UDon2 makes this possible via its n.prune(<rel>) and n.make_root() methods, where <rel> corresponds to the chain of dependency relations pointing at the node to be pruned.

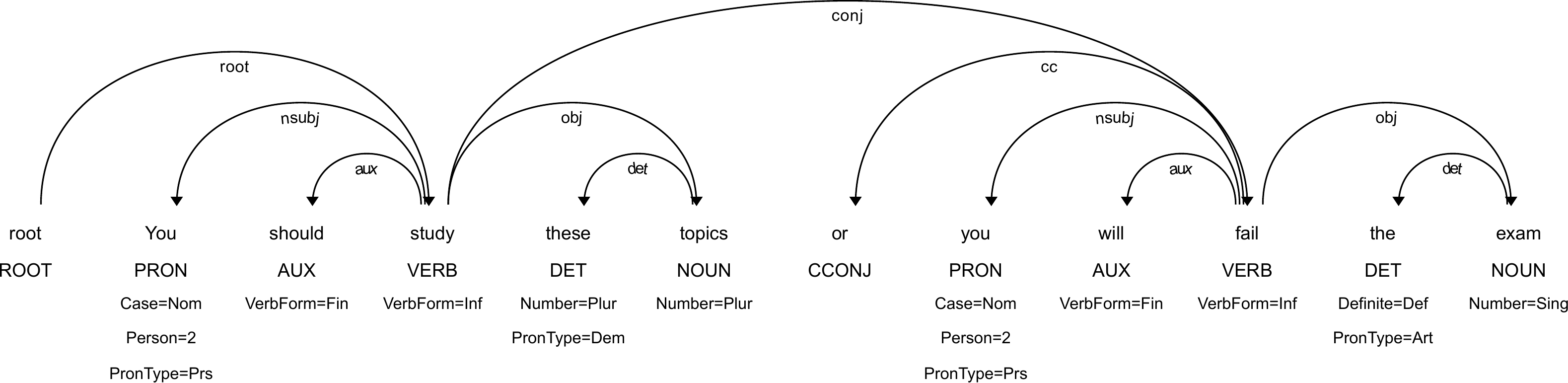To exemplify, consider the tree above and let r = root.children[0], then the following code is valid:

r.prune("conj")
r.make_root() # corresponds to the tree of "You should study these topics"

If the same tree is going to be used multiple times, destructive pruning might not be a viable option. In order to avoid copying trees, which might be a time-intensive (currently not implemented) operation, UDon2 allows ignoring individual nodes or subtrees by calling n.ignore(<label>) (n.ignore_subtree(<label>)), which assigns an ignore label <label> to n (all nodes in a subtree induced by n). All ignored nodes (no matter the label) will be excluded for all the queries presented in the previous section and during calling n.get_subtree_text().

Reverting to the original state, possible by calling n.reset(<label>) (n.reset_subtree(<label>)), will unignore only nodes with a matching ignore label. The <label> argument defaults to 0 for all mentioned methods. If all nodes should be reset (no matter the label), n.hard_reset() or n.hard_reset_subtree() should be used.

Grouping nodes

Nodes can be grouped based on their properties using n.group_by(prop) method, where prop is one of form, lemma, upos, xpos or deprel. The method returns udon2.GroupedNodes, which is basically a dictionary with a value of the selected property, as a key, and a udon2.NodeList of Nodes having the specified property with this key, as a value.

r.group_by("upos")
# returns a udon2.GroupedNodes equivalent to the following dict:
# {
#    'VERB': [Node<study>, Node<fail>],
#    'PRON': [Node<You>, Node<you>],
#    'AUX': [Node<should>, Node<will>],
#    'DET': [Node<these>, Node<the>],
#    'NOUN': [Node<topics>, Node<exam>],
#    'CCONJ': [Node<or>]
# }

Transformations

PCT, GRCT and LCT

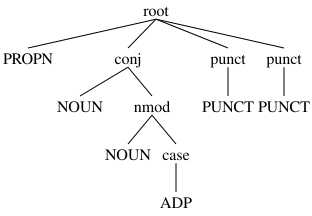
UDon2 allows transforming dependency trees to include edge labels as separate nodes into trees centered around PoS-tags (PCT), grammatical relations (GRCT) or lexicals (LCT), as introduced by Croce et al. (2011). To exemplify, consider the following tree.

The transformations can be applied using udon2.transform module as follows (assuming that n is the root node of the dependency tree above):

from udon2.transform import to_pct, to_grct, to_lct

grct = to_grct(n)
pct = to_pct(n)
lct = to_lct(n)

Since transformed trees have unlabeled edges, the familiar render_dep_tree function will not provide a good visualization. Hence, we introduce a new visualization function, namely render_tree.

from udon2.visual import render_tree
render_tree(pct, "pct.svg")
render_tree(grct, "grct.svg")
render_tree(lct, "lct.svg")

Note

When exporting SVG produced by render_tree to PNG or PDF, include the whole page and not only the drawing area by using the following command.

inkscape grct.svg --export-area-page --batch-process --export-type=png --export-filename=grct.png

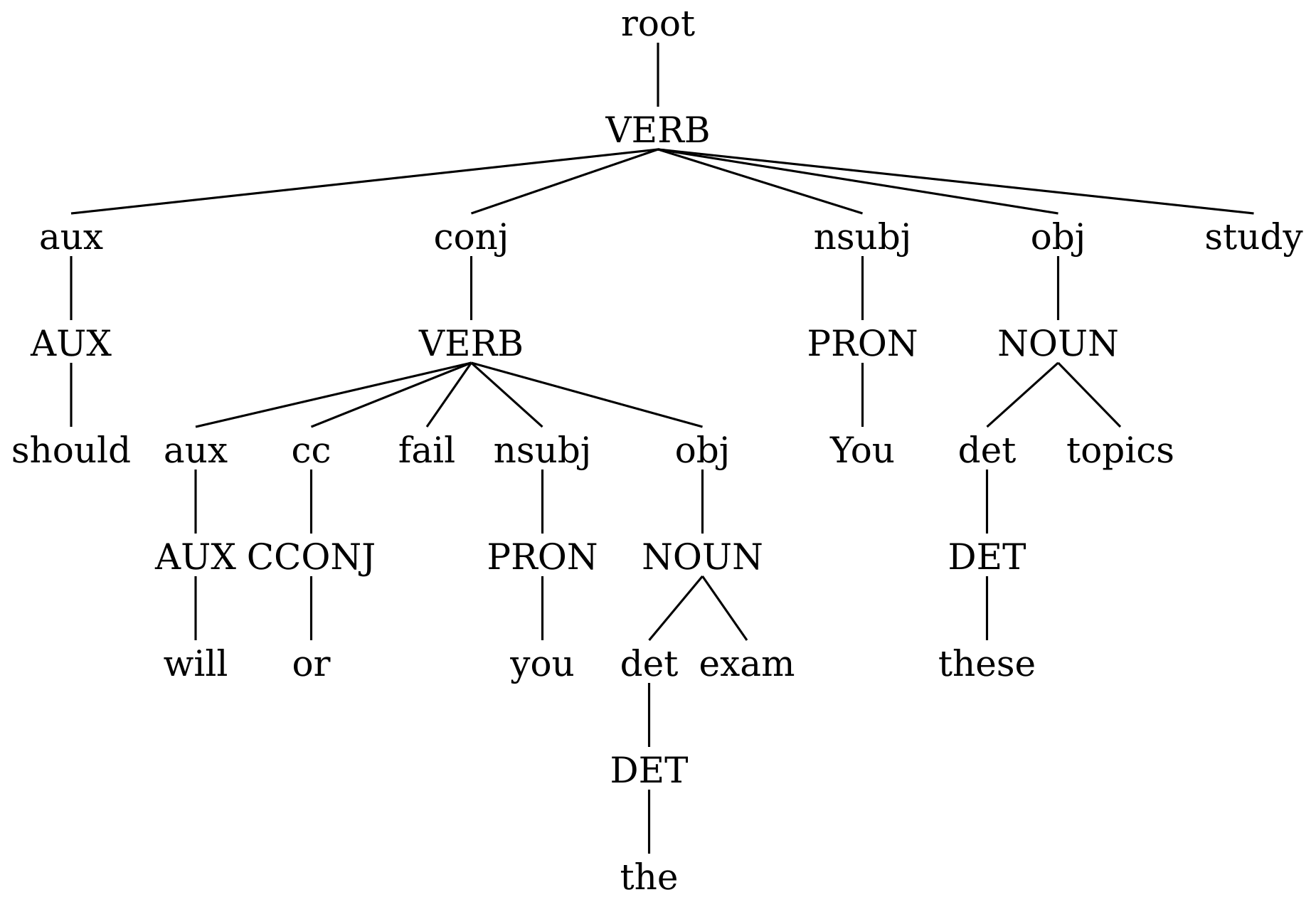
pct.svg

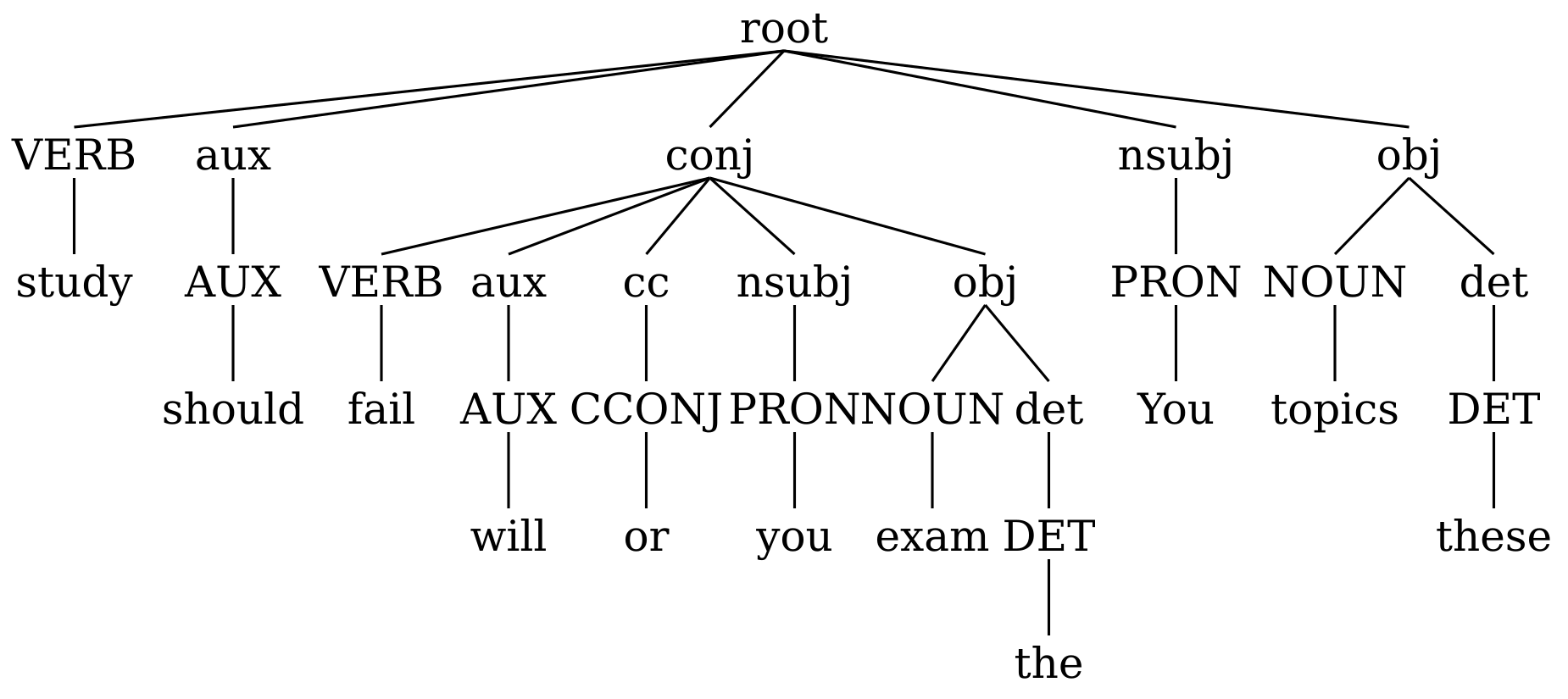
grct.svg

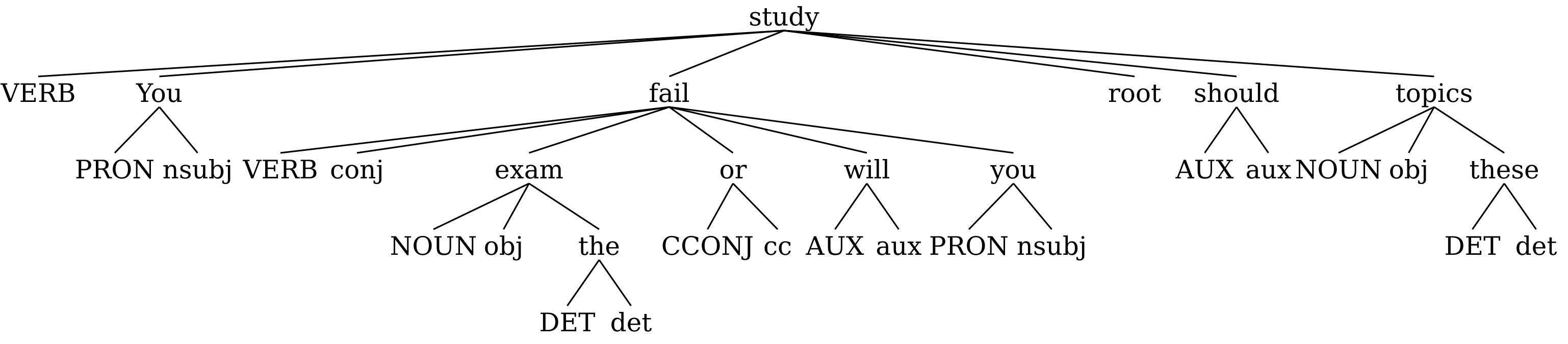
lct.svg

From v0.1b3

A possibility to include FEATS as a separate node and/or exclude FORM during transformations to PCT and GRCT is now added. LCT supports only including/excluding FEATS, since FORM is the backbone of this transformation. The examples below are shown only for GRCT.

from udon2.transform import to_pct, to_grct, to_lct

grct_with_feats = to_grct(n, includeFeats=True)
grct_wout_form = to_grct(n, includeForm=False)

render_tree(grct_with_feats, "grct_with_feats.svg")
render_tree(grct_wout_form, "grct_wout_form.svg")

grct_with_feats.svg

grct_wout_form.svg

Random distortion

From v0.1b3

Sometimes one needs to create dummy data from existing trees for training ML algorithms. UDon2 allows to do that using distort transformation. This transformation is performed over a number of comma-separated attributes (upos, deprel, lemma, and form), which are flipped with a specified probability p. upos and deprel will be randomly flipped to another valid value, whereas lemma and form will be replaced by a randomly generated string.

from udon2.transform import distort
p = 0.8 # probability to be distorted
n_distorted = distort(n, p, "upos,deprel,form")

Convolution kernels

It is non-trivial to represent dependency trees as features to use in machine learning contexts. One option was proposed by Moschitti (2006) in the form of convolution partial tree kernels that can be used with Support Vector Machines. In a nutshell, a partial tree kernel calculates the number of common tree structures (not only full subtrees) between two trees. Unfortunately, tree kernels cannot handle trees with labeled edges, which is why Moschitti (2006) applied kernels to dependency tree containing only lexicals. An alternative solution, as implemented in UDon2, is to re-format dependency trees to include the edge labels as separate nodes using the transformations defined in the previous section.

In UDon2, a partial tree kernel can be calculated in any of the aforementioned formats by substituting a string tree_format with any of "PCT", "GRCT" or "LCT" in the code snippet below.

from udon2.kernels import ConvPartialTreeKernel
# ptk_lambda and ptk_mu are decay factors as defined by Moschitti (2006)
kernel = ConvPartialTreeKernel(tree_format, ptk_lambda, ptk_mu)
# prints a number of common tree fragments between trees rooted at root1 and root2
print(kernel(root1, root2)) # root1 and root2 are udon2.Node instances

From v0.1b3

Convolution kernels now support new transformations including/excluding FEATS and FORM. These can be passed as keyword arguments (includeFeats is False by default and includeForm is True) to the constructor. Additionally mu and lambda also are available as keyword arguments, both having the value of 1 by default. Note that includeForm will have no influence on LCT transformation.

from udon2.kernels import ConvPartialTreeKernel
# ptk_lambda and ptk_mu are decay factors as defined by Moschitti (2006)
kernel = ConvPartialTreeKernel("GRCT", includeFeats=True, includeForm=False)
# prints a number of common tree fragments between trees rooted at root1 and root2
print(kernel(root1, root2)) # root1 and root2 are udon2.Node instances